SGISTL源码探究-stl_algo.h中的排列算法
前言
在本小节中,我们将分析
stl_algo.h
中的排列算法。可能你使用过STL中的
next_permutation
求过全排列。
比如这样:
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
int main()
{
string str;
cin >> str;
sort(str.begin(), str.end());
cout << str << endl;
while (next_permutation(str.begin(), str.end()))
{
cout << str << endl;
}
return 0;
}
next_permutation
的功能就是求出下一个排列,如果存在返回true,否则返回false。并且它会改变
[first, last)
序列,所以这样一直循环调用才能求出我们的全排列。
关于全排列算法,还有比较简单的递归版,实现的算法如下:
/* 假如求解(A, B, C, D)的全排列
* 1. 将A固定,求(B, C, D)的全排列
* 2. 将B固定,求(A, C, D)的全排列
* 3. 将C固定,求(A, B, D)的全排列
* 4. 将D固定,求(A, B, C)的全排列
* 然后再依次将问题化小,分别求解
*/
template <class BidirectionalIterator>
void full_permutation(BidirectionalIterator first, BidirectionalIterator last)
{
if(first == last)
{
//输出该排列
}
else
{
BidirectionalIterator cur = first;
while(cur++ != last)
{
swap(*first, *cur);
++first;
full_permutation(first, last);
--first;
swap(*first, *cur);
}
}
}
STL中的排列算法
SGISTL
中提供的计算排列组合的算法都是迭代版的,这种比起递归版的来说实现起来更复杂但是很稳定且效率比较高,分别是
next_permutation
和
prev_permutation
,即计算下一个排列以及前一个排列。
至于什么叫下一个排列,固定前几个元素,然后剩余的元素以字典序从小到大依次排列,剩下的元素排完之后,依据字典序从小到大更改固定的元素,继续排列,例如
abcd
,它的下一个排列就是
abdc
,固定了
ab
,接着剩下的
cd
排列的情况用完了,更改固定的元素为
ac
,继续排列。
通俗的来说就是每次让该排列的字典序大小最接近上一次排列,比如
acbd
的下一个排列即
acdb
。
next_permutation
该函数用于计算序列
[first, last)
的下一个排列,如果没有下一个排列,则返回falst,否则返回true。
template <class BidirectionalIterator>
bool next_permutation(BidirectionalIterator first,
BidirectionalIterator last) {
//区间为空,返回false
if (first == last) return false;
BidirectionalIterator i = first;
++i;
//若区间只有1个元素,返回false
if (i == last) return false;
//i指向最后一个元素
i = last;
--i;
/* 从末尾往前扫,寻找第一对递增的元素(i和ii)
* 若找到了,从末尾往前找第一个比i大的元素,将两者互换
* 由于`[ii, last)`可能是递减序列,所以我们需要将它翻转成递增序列,从而导致所求的下一个排列的字典序大小尽量靠近本排列,然后返回true
* 如果第一步中直到扫到了first都还是没有递增的元素,那就证明已经没有下一个排列了,翻转整个序列,返回false
*/
for(;;) {
//i和ii指向相邻的两个元素
BidirectionalIterator ii = i;
--i;
//寻找相邻的递增元素
if (*i < *ii) {
//j指向last
BidirectionalIterator j = last;
//寻找第一个比i大的元素
while (!(*i < *--j));
//交换
iter_swap(i, j);
//翻转[ii, last)的序列
reverse(ii, last);
return true;
}
//当抵达first时还没有相邻的递增元素
if (i == first) {
reverse(first, last);
return false;
}
}
}该算法对应了以下三种情况:
-
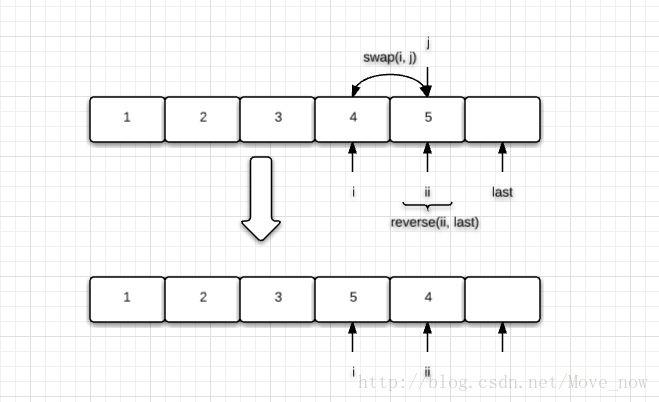
情况1:固定的元素不需要更改,对应图解如下
-
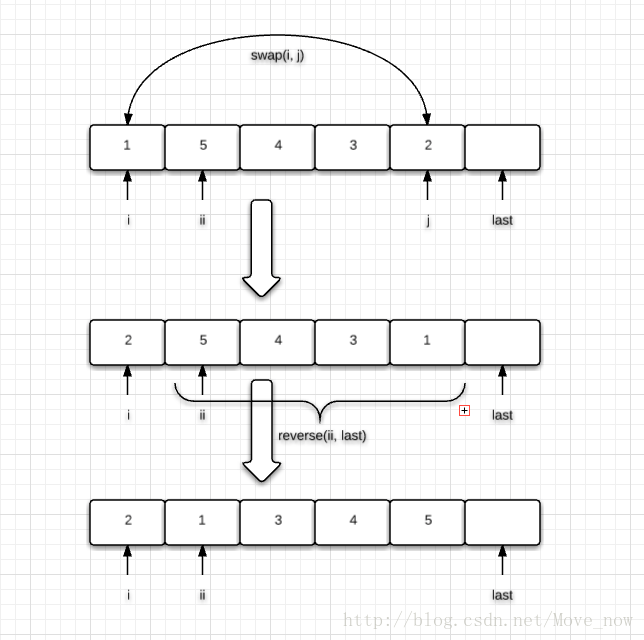
情况2:需要更改固定的元素,对应图解如下
-
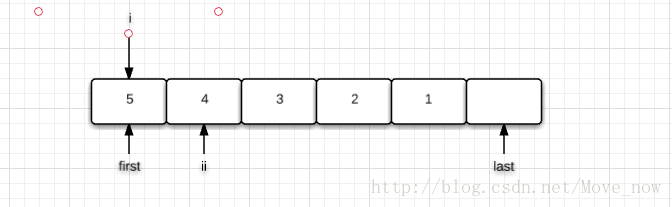
情况3:没有下一个排列的序列了,对应图解如下
prev_permutation
该算法用于求出前一个排列,它的实现与
next_permutation
十分相似,只是逻辑相反。
源码如下:
template <class BidirectionalIterator>
bool prev_permutation(BidirectionalIterator first,
BidirectionalIterator last) {
if (first == last) return false;
BidirectionalIterator i = first;
++i;
if (i == last) return false;
i = last;
--i;
for(;;) {
BidirectionalIterator ii = i;
--i;
//寻找相邻的递减元素
if (*ii < *i) {
BidirectionalIterator j = last;
//找到第一个比i小的元素
while (!(*--j < *i));
//交换i和j指向的元素
iter_swap(i, j);
//翻转
reverse(ii, last);
return true;
}
//直到扫到了first还未找到相邻的递减元素(即类似{1, 2, 3, 4, 5}这种情况),则退出
if (i == first) {
reverse(first, last);
return false;
}
}
}
小结
本小节分析了
next_permutation
以及
prev_permutation
算法的实现。如果觉得比较难理解,建议对照着图解和代码进行理解。接下来关于
stl_algo.h
中的算法,我们最后再分析其中的
sort
算法,至于其他的算法,剩下的也没几个了,后面就不一一分析了。