区间覆盖问题小结

大大源码 • • 其他

好像接触过不少区间覆盖类的问题了，写个博客小结一下。

1，求最大覆盖次数

问题描述：相当于给你一些区间，每次给这些区间内的点值都加一（初始都为0），然后问最大的值是多少。（也就是单点的最大覆盖次数）

解决思路：显然树状数组可以很好地解决，复杂度nlogn，显得有些大材小用了。现在有一个好写复杂度还低一点的办法：把所有区间的左端点标为1，右端点标为-1，再从头到尾遍历一遍加上当前点的值，维护ans为最大值即可。

tips:为了防止一个区间的右端点和另一个的左端点重合导致答案错误，采取r++操作，可以证明不会影响结果。

代码实现：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<string>
#include<iomanip>
#include<map>
#include<vector>
#include<set>
#include<queue>
#include<stack>
#define FAST ios::sync_with_stdio(false)
#define lowbit(x) x&(-x)
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 7;
const int maxn = (int)1e5 + 5;
using namespace std;

int a[maxn];

int main()
{
	int n, m;//区间范围为1-n,给m个区间
	cin >> n >> m;
	while(m--){
		int l, r;
		cin >> l >> r;
		a[l]++, a[r+1]--;
	}
	int t = 0, ans = -inf;
	for(int i = 1; i <= n; i++){
		t += a[i];
		ans = max(ans, t);
	}
	cout << ans << endl;
	return 0;
}

2，求最多不相交区间

问题描述：经典例题：一个人要参加一些会议，给你这些会议的开始和结束时间，问你他最多能参加多少会议。

解题思路：贪心的思想做。贪心策略：哪个越早结束就先参加哪个。结构体排序，按结束时间排，再贪心遍历求解即可。

代码实现：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<string>
#include<iomanip>
#include<map>
#include<vector>
#include<set>
#include<queue>
#include<stack>
#define FAST ios::sync_with_stdio(false)
#define lowbit(x) x&(-x)
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 7;
const int maxn = (int)1e5 + 5;
using namespace std;

struct hia{
	int l, r;
};

bool cmp(hia x, hia y){
	return x.r < y.r;
}

hia z[maxn];

int main()
{
	int n, m;
	scanf("%d %d", &n, &m);
	for(int i = 1; i <= m; i++)
		scanf("%d %d", &z[i].l, &z[i].r);
	sort(z + 1, z + m + 1, cmp);
	int pos = 0, sum = 0;
	for(int i = 1; i <= m; i++)
		if(z[i].l >= pos){
			pos = z[i].r;
			sum++;
		}
	printf("%d\n", sum);
	return 0;
}

例题：略略略

3，求被覆盖i次的点的个数

问题描述：给你n个区间，分别求出被覆盖1-n次的点的个数

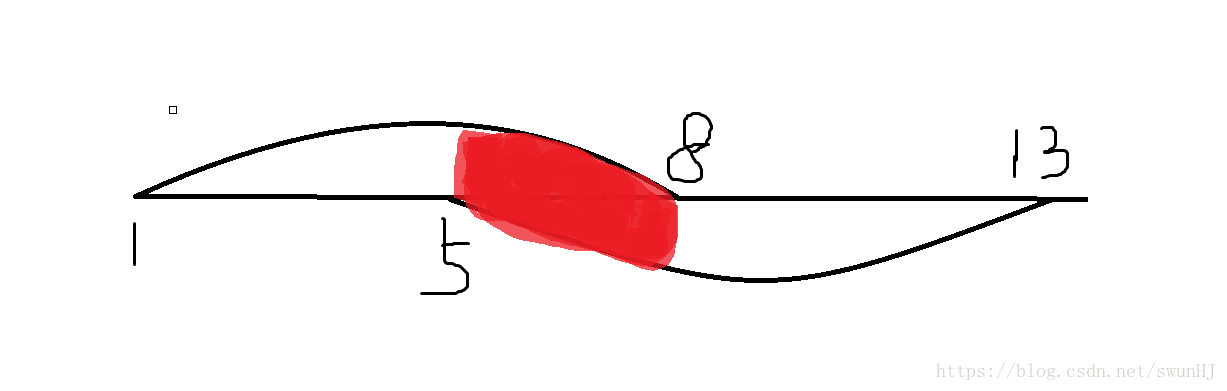
解题思路：把端点从小到大排个序，左端点标个1，右端点标个-1（实际上是右端点的后面一位，避免左端点和另一个的右端点重合情况的干扰），从左到右扫一遍，这样就能很方便地求出不同区间覆盖次数的值。

 

 

如图，给两个区间[1,7], [5, 12],用now记录当前我们加的前缀和，我们在遍历到5的时候，有cnt[1] += (5-3),（now ==1）遍历到8的时候,cnt[2] += (8 - 5)，(now == 2)（其实这里是区间[5,7]的贡献，这也能解释为什么在标记的时候标记右端点的后一位），再遍历到13，cnt[1] += (13 - 8)，(now == 1)。这样就能很好的完成记录。

代码：（用map显然更方便一点）

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<string>
#include<iomanip>
#include<map>
#include<vector>
#include<set>
#include<queue>
#include<stack>
#define FAST ios::sync_with_stdio(false)
#define lowbit(x) x&(-x)
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 7;
const int maxn = (int)2e5 + 5;
using namespace std;

map<ll, int> m;

ll cnt[maxn];

int main()
{
	int n; scanf("%d", &n);
	for(int i = 0; i < n; i++){
		ll a, b;
		cin >> a >> b;
		m[a]++;
		m[b+1]--;
	}
	int now = 0;
	ll t = 0;
	map<ll, int>::iterator it;
	for(it = m.begin(); it != m.end(); it++){
		ll x = it->first;
		cnt[now] += (x - t);
		now += it->second;
		t = x;
	}
	for(int i = 1; i < n; i++)
		printf("%lld ", cnt[i]);
	printf("%lld\n", cnt[n]);
	return 0;
}

例题：Cross Fire!!!

4,求最少的能覆盖区间的区间数

大意：给一个区间[L, R]，再给一些[l[i], r[i]]，求用这些区间覆盖[L, R]的最少数目

解决思路：贪心解决。把这些区间以左端点进行排序，先选择第一个区间，之后的贪心策略就是选择在可选范围内的，选择右端点最大的区间。

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<string>
#include<iomanip>
#include<map>
#include<vector>
#include<set>
#include<queue>
#include<stack>
#define FAST ios::sync_with_stdio(false)
#define lowbit(x) x&(-x)
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 7;
const int maxn = 25005;
using namespace std;

struct hia{
	int l, r;
} a[maxn];

bool cmp(hia x, hia y){
	return x.l < y.l;
}

int main()
{
	int n, t; scanf("%d %d", &n, &t);
	for(int i = 0; i < n; i++){
		scanf("%d %d", &a[i].l, &a[i].r);
	}
	sort(a, a + n, cmp);
	int ans = 0, i = 0, temp = 0;
	while(temp < t && i < n){
		ans++;
		int top = temp;
		if(a[i].l > temp + 1) return 0*puts("-1");
		while(i < n && a[i].l <= temp + 1){
			top = max(top, a[i].r);
			i++;
		}
		temp = top;
	}
	if(temp < t) puts("-1");
	else printf("%d\n", ans);
	return 0;
}

（此代码可 AC   POJ2376）http://poj.org/problem?id=2376

 

5，求一段区间覆盖了多少个其他的区间

大意：给你一些区间，有一些询问，每次询问给一个区间，输出这个区间覆盖了多少区间

解题思路：用二维前缀和来做。一个区间用a[l, r]来表示。询问的时候就相当于求[l, l] 到 [r, r]这个矩形中的元素数目

即sum[r][r] - sum[r][l-1] - sum[l-1][r] + sum[l-1][l-1]

#include<set>
#include<map>
#include<cmath>
#include<ctime>
#include<queue>
#include<cstdio>
#include<string>
#include<vector>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<algorithm>
#define fi first
#define se second
#define pb push_back
#define lowbit(x) x&(-x)
#define PII  pair<int, int> 
#define all(x) x.begin(), x.end()
#define FAST ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 7;
const int maxn = (int)150000 + 5;
using namespace std;

int sum[505][505];

int main()
{
	int n, m, q; scanf("%d %d %d", &n, &m, &q);
	int l, r;
	for(int i = 1; i <= m; i++){
		scanf("%d %d", &l, &r);
		sum[l][r]++;
	}
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){
			sum[i][j] += sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1];
		}
	}
	while(q--){
		scanf("%d %d", &l, &r);
		printf("%d\n", sum[r][r] - sum[r][l-1] - sum[l-1][r] + sum[l-1][l-1]);
	}
	return 0;
}

例题：D - AtCoder Express 2

版权声明：本文为swunHJ原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
THE END
< <上一篇
下一篇>>