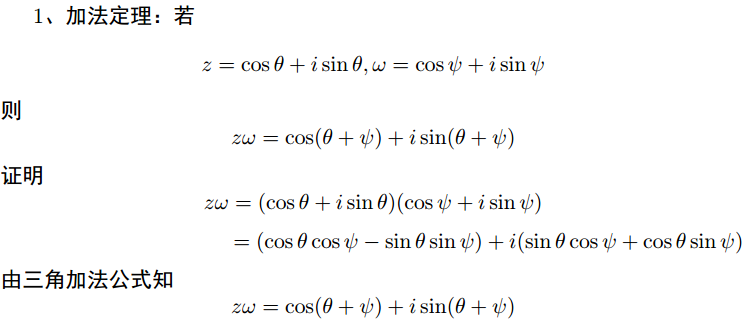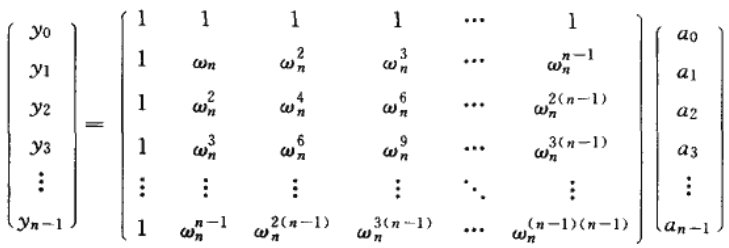多项式与快速傅里叶变换（FFT）

参考：《算法导论》第 30 章 多项式与快速傅里叶变换

《华章数学译丛-抽象代数基础教程.(美国)Rotman》第 1 章 数论

http://blog.csdn.net/liangzhaoyang1/article/details/52769839

《叉姐的FFT讲义》

一、概述

两个多项式相乘的简单方法所需的时间为 O(n ^ 2)

快速傅里叶变换（Fast Fourier Transform，FFT）方法可以使多项式相乘的运行时间降低为 O(logn)

二、

1、多项式

关于变量 x 的多项式定义为形式和形式表示的函数 A(x)：

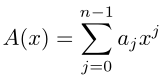
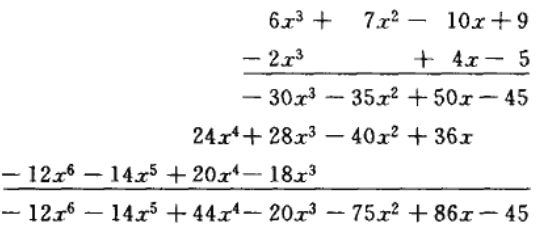
2、多项式的系数表示法

3、多项式的点值表示法

3、插值

三、系数形式表示的多项式的快速乘法

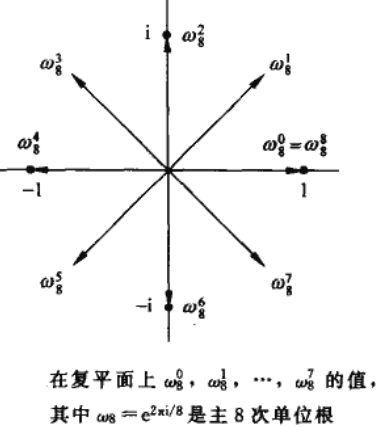
四、DFT 与 FFT

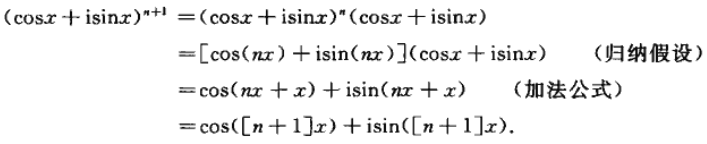
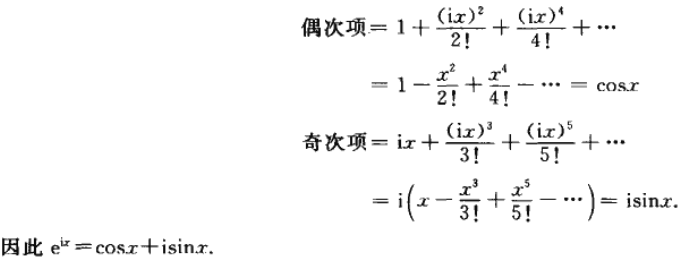
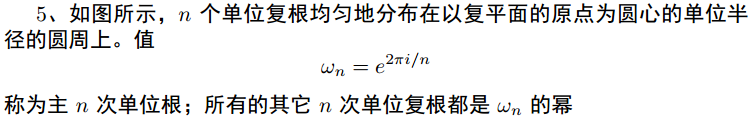
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <cmath>
#include <cctype>
#include <ctime>

using namespace std;

#define REP(i, n) for (int i = 0; i < (n); ++i)
#define PI acos(-1.0)

const int maxn = 3e5 + 10;

struct Complex {
    double x, y;
    Complex(double _x = 0.0, double _y = 0.0) { x = _x; y = _y; }
    Complex operator - (const Complex &b) const { return Complex(x - b.x, y - b.y); }
    Complex operator + (const Complex &b) const { return Complex(x + b.x, y + b.y); }
    Complex operator * (const Complex &b) const { return Complex(x * b.x - y * b.y, x * b.y + y * b.x); }
};

int poly_A[maxn / 3], poly_B[maxn / 3];
Complex A[maxn], B[maxn], ans_mul[maxn];
int N, M, n = 1;

Complex* fft(Complex a[], int len, int oper);

int main() {
#ifdef __AiR_H
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif // __AiR_H
    scanf("%d %d", &N, &M);
    REP(i, N + 1) { scanf("%d", &poly_A[i]); }
    REP(i, M + 1) { scanf("%d", &poly_B[i]); }
    while (n < N + M + 2) { n <<= 1; }
    REP(i, N + 1) { A[i] = poly_A[i]; }
    for (int i = N + 1; i < n; ++i) { A[i] = 0; }
    REP(i, M + 1) { B[i] = poly_B[i]; }
    for (int i = M + 1; i < n; ++i) { B[i] = 0; }
    Complex *ans_A = new Complex[n], *ans_B = new Complex[n], *ans = new Complex(n);
    ans_A = fft(A, n, 1); ans_B = fft(B, n, 1);
    REP(i, n) { ans_mul[i] = ans_A[i] * ans_B[i]; }
    ans = fft(ans_mul, n, -1);
    REP(i, n) { ans[i].x /= n; ans[i].y /= n; }
    REP(i, N + M ) { printf("%.0f ", fabs(ans[i].x)); } printf("%.0f\n", fabs(ans[N + M].x));
#ifdef __AiR_H
    printf("Time used = %.2fs\n", (double)clock() / CLOCKS_PER_SEC);
#endif // __AiR_H
    return 0;
}

Complex* fft(Complex a[], int len, int oper) {
    if (len == 1) { return a; }
    Complex omega_n = Complex(cos(oper * 2.0 * PI / len), sin(oper * 2.0 * PI / len));
    Complex omega = Complex(1, 0);
    Complex* a_0 = new Complex[len >> 1];
    Complex* a_1 = new Complex[len >> 1];
    REP(i, len) { (i & 1) ? (a_1[(i - 1) >> 1] = a[i]) : (a_0[i >> 1] = a[i]); }
    Complex *y_0, *y_1;
    y_0 = fft(a_0, len >> 1, oper); y_1 = fft(a_1, len >> 1, oper);
    Complex* y = new Complex[len];
    for (int i = 0; i < (len >> 1); ++i) {
        y[i] = y_0[i] + omega * y_1[i];
        y[i + (len >> 1)] = y_0[i] - omega * y_1[i];
        omega = omega * omega_n;
    }
    return y;
}

UOJ #34. 多项式乘法

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <cmath>
#include <cctype>
#include <ctime>

using namespace std;

#define REP(i, n) for (int i = 0; i < (n); ++i)
#define PI acos(-1.0)

const int maxn = 3e5 + 10;

struct Complex {
    double x, y;
    Complex(double _x = 0.0, double _y = 0.0) { x = _x; y = _y; }
    Complex operator - (const Complex &b) const { return Complex(x - b.x, y - b.y); }
    Complex operator + (const Complex &b) const { return Complex(x + b.x, y + b.y); }
    Complex operator * (const Complex &b) const { return Complex(x * b.x - y * b.y, x * b.y + y * b.x); }
};

int poly_A[maxn / 3], poly_B[maxn / 3];
Complex A[maxn], B[maxn], ans[maxn];
int N, M, n = 1;

void fft(Complex a[], int len, int oper);

int main() {
#ifdef __AiR_H
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif // __AiR_H
    scanf("%d %d", &N, &M);
    REP(i, N + 1) { scanf("%d", &poly_A[i]); }
    REP(i, M + 1) { scanf("%d", &poly_B[i]); }
    while (n < N + M + 2) { n <<= 1; }
    REP(i, N + 1) { A[i] = poly_A[i]; }
    for (int i = N + 1; i < n; ++i) { A[i] = 0; }
    REP(i, M + 1) { B[i] = poly_B[i]; }
    for (int i = M + 1; i < n; ++i) { B[i] = 0; }
    fft(A, n, 1); fft(B, n, 1);
    REP(i, n) { ans[i] = A[i] * B[i]; }
    fft(ans, n, -1);
    REP(i, N + M) { printf("%.0f ", fabs(ans[i].x)); } printf("%.0f\n", fabs(ans[N + M].x));
#ifdef __AiR_H
    printf("Time used = %.2fs\n", (double)clock() / CLOCKS_PER_SEC);
#endif // __AiR_H
    return 0;
}

void fft(Complex a[], int len, int oper) {
    for (int i = 1, j = 0; i < len - 1; ++i) {
        for (int s = len; ~j & s;) { j ^= s >>= 1; }
        if (i < j) { swap(a[i], a[j]); }
    }
    Complex omega_m, omega, t, u;
    int m, m2;
    for (int d = 0; (1 << d) < len; ++d) {
        m = (1 << d); m2 = m << 1;
        omega_m = Complex(cos(PI / m * oper), sin(PI / m * oper));
        for (int i = 0; i < len; i += m2) {
            omega = Complex(1, 0);
            for (int j = 0; j < m; ++j) {
                u = a[i + j]; t = omega * a[i + j + m];
                a[i + j] = u + t; a[i + j + m] = u - t;
                omega = omega * omega_m;
            }
        }
    }
    if (oper == -1) { REP(i, N + M + 1) { a[i].x /= len; } }
}