分治法

分治法基本就是下面的三步

1. 分(divide)：无法有效解决的划分更小的问题
2. 治(conquer)：递归求每一个子问题的解
3. 合(combine)：合并解得出原问题解

MergeSort：排列

1. Divide: Use index
2. conquer  recursively sort each subarray
3. combine  two sorted arrays Θ(n)

T(n)=2T(n/2)+ Θ(n) > Θ(nlgn) （master method case 2）

QuickSort：排列

1. Divide: Partion array into two subarray ,and pivot x $elems Lower subarr≤x≤upperarr
2. conquer  recursively sort tow subarray
3. combine  Not needed

Worst-case：正向或者逆向排好
T(n)=T(n-1)+ T(0)+Θ(n)=T(n-1)+Θ(n) > Θ(²)
注：T(n)=T(n-1)+Θ(n) 是等差，所以为 Θ(²)

Best-case：划分为两半
T(n)=2T(n/2)+ Θ(n) > Θ(nlgn)

划分是常数比例的都是Θ(nlgn)

Binary Search : 在有序表中找X

1. Divide: compare x with middle
2. conquer  recursively in one subarray
3. combine Not Needed

T(n)=T(n/2)+ Θ(1) > Θ(lgn) （master method case 2）

Powering a number : 求 xⁿ

if n = even: xⁿ=x^n/2x^n/2
if n = odd: xⁿ=x^(n-1)/2 + x^(n-1)/2 x

T(n)=T(n/2)+ Θ(1) > Θ(lgn)

Fibonaci number

F₀=0 ,F₁=1，F_n=F_n-1+F_n-2(n>2)
Ω(φⁿ) 其中 φ=(√5+1/)2
利用递归式使用分治法运行时间是指数级的，不好，仔细看规模，都是减小1或者2，几乎没有降低，且蕴含大量重复计算

这时候使用分治法有点不好，我们使用从下至上或者动态规划
从上至下(Button-to-Top)：依次计算F₀，F₁，…，F_n，因为可以直接用前面两项的求后一项 Θ(n)

朴素平凡递归式
F_n=（φⁿ/√5） 取最近的整数，利用分治法Θ(lgn)求出φⁿ
这种实现不了，因为计算机浮点数运算有精度问题，最近取整得不到正确答案

平凡递归算法
Recursive Squaring

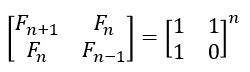
这就又归结于xⁿ的求法，所以可以在lgn时间内求出F_n（因为固定2X2的矩阵所以这里求矩阵是常数时间）

矩阵求法

可以使用分治的理由，矩阵的分块乘法
n X n 分解成几个 n/2 X n/2，如下我们分解每个矩阵成四块

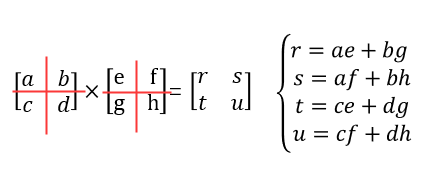
然后 ae，bg，af，bh，ce，dg，cf，dh又是矩阵乘法，然后递归求这几个

T(n)=8T(n/2)+ Θ(n²) > Θ(n³)
注：ae+bg 矩阵加法所耗费的时间为Θ(n²)

上面的方法并不好
Strassen’s Algo
Strassen 想出了7次递归的算法，与上面得方法在于求r,s,t,u不同，如下求出，只要7次矩阵乘法

1. Divide    A，B，compute all p
2. conquer  recursively compute p
3. combine  r,s,t,u

T(n)=7T(n/2)+ Θ(n²) > Θ(n^log27)≈ Θ(n^2.81)

目前最快为 Θ(n^2.376)，但是纯理论的提升，不能用

摘自《算法导论》

分治法求解递推式

一丶代入法

1. 猜测解的形式
2. 用数学归归纳法求出解中的常数，并证明解是正确的

需要注意：并不存在通用的方法来猜测递归式的正确解，猜测解需要靠经验，偶尔还需要创造了

二丶采用递归树

这是一种简单而直接的方法来设计好的猜测解，再使用代入法验证猜测是否正确
以下面为例

三丶主方法求解

类似于菜谱，带入公式求解