冒泡、简单选择、直接插入、希尔、快速、归并、堆排序算法:JavaScript实现+分析
补充:动态规划与分治法的本质区别
① 分治法将分解后的子问题看成相互独立的。
② 动态规划将分解后的子问题理解为相互间有联系,有重叠部分。
| 算法 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 排序方式 | 稳定性 | 算法设计策略 |
|---|---|---|---|---|---|---|
| 冒泡【交】 | n【flag判是否交换】 | n2 | 1 | 内 | 稳定 | |
| 选择 | n2 | n2 | 1 | 内 | 不稳定 | |
| 插入 | n【基本有序】 | n2 | 1 | 内 | 稳定 | |
| 希尔【插入】 | 与增量相关还在研究 | n2 | 1 | 内 | 不稳定 | |
| 归并 | nlogn | nlogn | n | 外 | 稳定 | 分治 |
| 快速【交换】 | nlogn | n2【有序】 | logn~n | 内 | 不稳定 | 分治 |
| 堆【选择】 | 稳定 |
通常说空间复杂度一般指的是额外空间复杂度。
k: “桶”的个数
冒泡
n 次比较相邻两数并交换(将较大数放在右边),实现将最值放在末尾,
然后 n-1 次比较找到次值……较小的数字像气泡一样浮出。
这里我引入flag排除:已经有序却一直遍历
function bubbleSort(arr){
const n=arr.length;
let flag=1,i,j;
for(i=0;i<n-1&&flag;i++){
//最坏的情况需要依次比较出最小值、次小值、次次小值
flag=0;//如果交换了就变
for(j=0;j<n-i-1;j++){
if(arr[j]>arr[j+1]){
const swap=arr[j];
arr[j]=arr[j+1];
arr[j+1]=swap;
flag=1;
}
}
}
return arr;
}
简单选择排序
和冒泡原理相似,但是少了很多交换,多了一个暂存最值的空间。
n 次比较相邻两数后最多只交换一次将最值放到位置上,然后 n-1 次比较找到次值
冒泡更适合基本有序的序列
function selectSort(arr)
{
const n=arr.length;
let i,j,minIndex;
for(i=0;i<n-1;i++){
minIndex=i;//先决定谁最小
for(j=i+1;j<n;j++){
if(arr[j]<arr[minIndex]){
minIndex=j;
}
}
if(minIndex!=i){
const swap=arr[i];
arr[i]=arr[minIndex];
arr[minIndex]=swap;
}
}
return arr;
}
直接插入
维护一个渐长的有序队列
function insertSort(arr)
{
const n=arr.length;
let i,j,k;
for (i = 1; i < n; i++)//单个数据==有序,从第二个数开始插入
{
// a[i]插入前面的有序区间a[0...i-1]
for (j = i - 1; j >= 0; j--){
if (arr[j] < arr[i])break;
}
//这里有两种可能,需要插入前面、不需要
if (j != i - 1){//需要插入
//后移一位,空出位置给arr[i]
const temp = arr[i];
for (k = i - 1; k > j; k--)
arr[k + 1] = arr[k];
//将a[i]放到正确位置上
arr[k + 1] = temp;
}
}
return arr;
}
希尔排序(进阶版插入)
相比直接插入,多了一个维度。
利用gap划分小组
gap由大变小
每个小组进行直接插入排序

注意呀,JavaScript除法没有默认取整,需要借助parseInt方法
function shellSort(arr)
{
const n=arr.length;
let i, j, gap;
for (gap =parseInt(n/2); gap> 0; gap=parseInt(gap/2)){//依次缩小比较间隙
for (i = gap; i < n; i++){//gap分组
for (j = i - gap; j >= 0 && arr[j] > arr[j + gap]; j -= gap){//每个分组进行插入排序
console.log("j:"+j);
const temp=arr[j + gap];
arr[j + gap]=arr[j];
arr[j]=temp;
}
}
}
return arr;
}
动态间隔序列的希尔
function shellsort(array) {
var N = array.length;
var h = 1;
while (h < N/3) {
h = 3 * h + 1;
}
while (h >= 1) {
for (var i = h; i < N; i++) {
for (var j = i; j >= h && array[j] < array[j-h];
j -= h) {
[array[j],array[j-h]]=[array[j-h],array[j]]
}
}
h = (h-1)/3;
}
return array;
}
let nums=[1,5,3,6,3,2,9,1];
console.log(shellsort(nums));
快速排序
适合大型数据,小型数据性能反而会下降
平均时间复杂度=O(n logn)
序列基本有序状态时,快速排序退化为O(n^2)
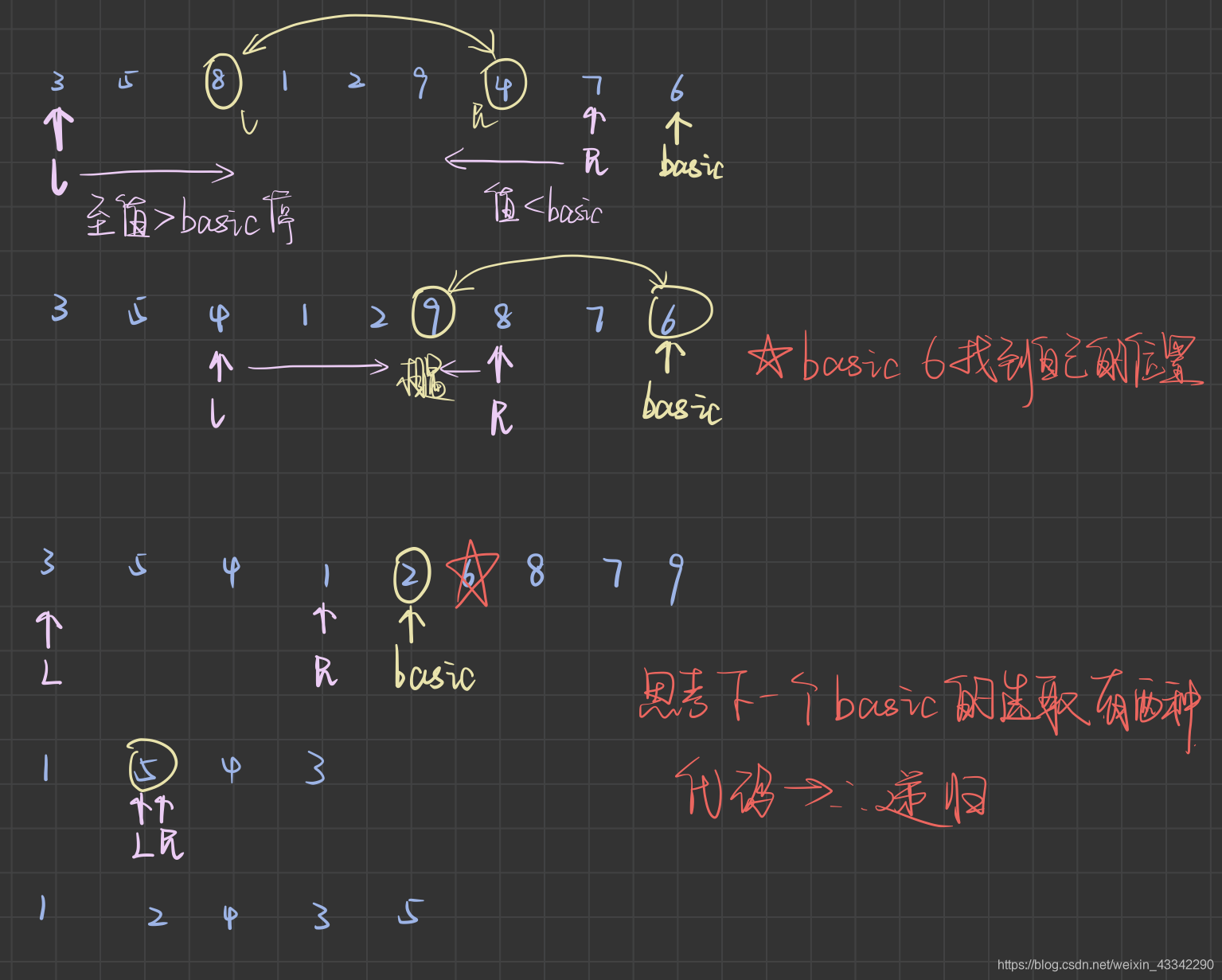
function quick_part(arr,left,right){
//留下left和right后面递归
var l = left;
var r = right;
var basic= arr[left]; //arr[left]即basic的原位置
if(left >= right){ //如果数组只有一个元素
return;
}
while(l!=r){//两者相遇,意味着一直到找到basic的位置
while(arr[r] > basic && l < r){ //l<r随时注意严格控制哨兵不能错过,从右边向左找第一个比key小的数,找到或者两个哨兵相碰,跳出循环
r--;
}
while(arr[l] <= basic && l < r){ //这里的=号保证在本轮循环结束前,key的位置不变,否则的话跳出循环,交换l和left的位置的时候,left位置的上元素有可能不是key
l++;
}
//1、两个哨兵到找到了目标值。2、j哨兵找到了目标值。3、两个哨兵都没找到(key是当前数组最小值)
if(l!=r){ //交换两个元素的位置
const swap = arr[l];
arr[l] = arr[r];
arr[r] = swap;
}
}
arr[left] = arr[l] //arr[left]即basic的原位置
arr[l] = basic;
quick_part(arr,left,l-1);
quick_part(arr,l+1,right);
}
function quickSort(arr){
quick_part(arr,0,arr.length-1);
}
function qSort(arr)
{
if (arr.length == 0) {
return [];
}
var left = [];
var right = [];
var pivot = arr[0];
for (var i = 1; i < arr.length; i++) {
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return qSort(left).concat(pivot, qSort(right));
}
var a = [];
for (var i = 0; i < 10; ++i) {
a[i] = Math.floor((Math.random()*100)+1);
}
console.log(qSort(a));
归并排序

function merge(left,right){
var temp=[];
while(left.length&&right.length){//取小的
if(left[0]<right[0]){
temp.push(left.shift());
}else{
temp.push(right.shift());
}
}
console.log("s:"+temp);
//left和right长度不一样时,直接连接剩下的长的部分(本身有序)
return temp.concat(left,right);
}
function mergeSort(arr){
if(arr.length<=1){
return arr;//打破后面return中的递归,有返回值了就去执行merge
}
var mid=Math.floor(arr.length/2);//
var left=arr.slice(0,mid);
var right=arr.slice(mid);
i++;
console.log(i+":"+left+right);
return merge(mergeSort(left),mergeSort(right));
}
堆排序
JavaScript的除法不是整除,另外提供了不同的取整方法
大顶堆的分析:
- 数组映射堆的下标分析
- 过程分析(结合代码)

大顶堆的代码实现
var len; //全局的len,控制大顶堆的长度,实现在原数组上的调整
function swap(arr, i, j) {
const temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function heapSort(arr) {
//通用方法
function maxHeapify(arr, i) { //调整以i为根的树为大顶堆,
var left = 2*i+1,
right = 2*i+2,
largest = i; //暂定根节点最大
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) { //当该树不知三个节点的时候,如果做出了调整可能破坏了子的大顶堆,需要条件递归
swap(arr, i, largest); //交换最大的为父节点
maxHeapify(arr, largest); //交换后,原值arr[i](往下降了)(索引保存为largest)
//作为根时,子节点可能比它大,因此要继续调整
//往下查看
}
}
//构建大顶堆
function buildMaxHeap(arr) { //对每一个节点(非叶节点),做堆调整
len = arr.length;
//从最后一个有子节点开始,构建是自底向上的
for (var i = Math.floor(len/2)-1; i>=0; i--) {
maxHeapify(arr, i);
}
}
//输出顺序,并不断维持大顶堆
function orderQ(arr) {
//把最大的数放到最后,然后全局len--=》让大顶堆减少一个数,再调整维持大顶堆
for (var i = arr.length-1; i > 0; i--) {
swap(arr, 0, i);
len--;
maxHeapify(arr, 0);
}
}
buildMaxHeap(arr);
orderQ(arr);
return arr;
}
同理小顶堆的代码:
var len; //全局的len,控制大顶堆的长度,实现在原数组上的调整
function swap(arr, i, j) {
const temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function heapSort(arr) {
//通用方法
function minHeapify(arr, i) { //调整以i为根的树为大顶堆,
var left = 2*i+1,
right = 2*i+2,
minest = i; //暂定根节点最大
if (left < len && arr[left] <arr[minest]) {
minest = left;
}
if (right < len && arr[right] <arr[minest]) {
minest = right;
}
if (minest != i) { //当该树不知三个节点的时候,如果做出了调整可能破坏了子的大顶堆,需要条件递归
swap(arr, i, minest); //交换最大的为父节点
minHeapify(arr, minest); //交换后,原值arr[i](往下降了)(索引保存为largest)
//作为根时,子节点可能比它大,因此要继续调整
//往下查看
}
}
//构建大顶堆
function buildMinHeap(arr) { //对每一个节点(非叶节点),做堆调整
len = arr.length;
//从最后一个有子节点开始,构建是自底向上的
for (var i = Math.floor(len/2)-1; i>=0; i--) {
minHeapify(arr, i);
}
}
//输出顺序,并不断维持大顶堆
function orderQ(arr) {
//把最大的数放到最后,然后全局len--=》让大顶堆减少一个数,再调整维持大顶堆
for (var i = arr.length-1; i > 0; i--) {
swap(arr, 0, i);
len--;
minHeapify(arr, 0);
}
}
buildMinHeap(arr);
orderQ(arr);
return arr;
}
版权声明:本文为weixin_43342290原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。