复数特征值求特征向量_Lecture 20 | 特征值与特征向量

本节是n阶矩阵的性质或作用。

矩阵A作用在向量x上，表现形式为Ax，这类似于函数f(x)：函数f(x)与x一一对应，而向量Ax则是多维关系下与向量x一一对应。

矩阵A的作用就像输入一个向量x，输出一个新向量Ax。输出向量必然与输入向量存在某种联系，当然输入向量x也一定有所限制(类比函数有定义域)。

01

Eigenvector

特征向量

如果给定一个向量x，和一个方阵A，如果向量Ax与x保持平行关系，则称这个向量x为矩阵的特征向量。

Ax∥x，这样的向量x会有无数个，这些向量统统都是矩阵A的特征向量。

02

Eigenvalue

特征值

这个概念由上面的平行关系引出，当向量a与向量b平行时，可以用a=λb这样的数学形式表示。

故当Ax与x平行时，可以写成Ax=λx。

这里的λ就是特征值，且一个特征向量对应一个特征值。

关于向量平行的关系中要注意0向量，它与任何向量平行，矩阵A作用在零向量上得到的依旧是0向量，但特征值就可能会有无数个，所以0向量在这里没什么太大意义。

Example

①投影矩阵的特征向量和特征值

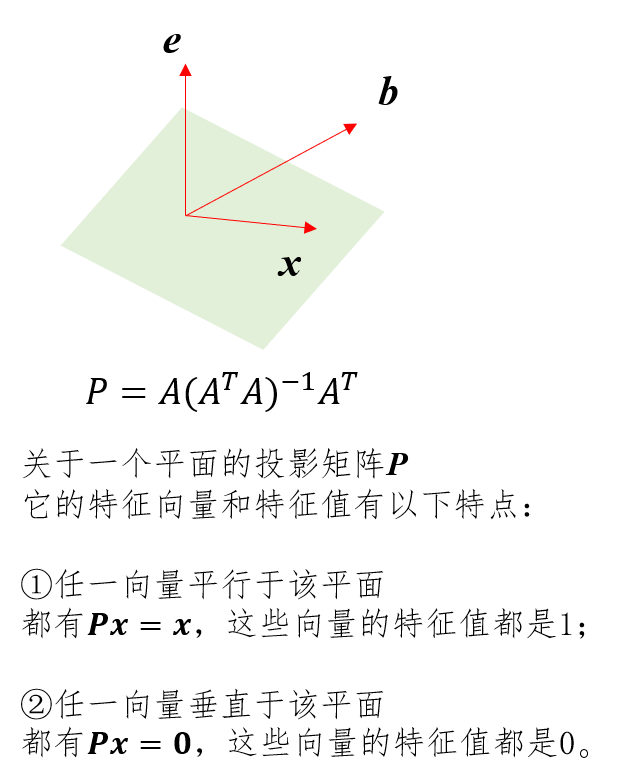
②置换矩阵的特征向量和特征值

③奇异矩阵的特征向量和特征值

如果矩阵A不可逆的话，那么总可以找到一个非0向量x，使得Ax=0，因此0一定是奇异矩阵的一个特征值。

Key

如何求解特征值与特征向量？

这个问题的关键在于求解Ax=λx

将上述方程稍微改动，移项通分可得：

(A-λI)x=0

从上面的奇异矩阵的例子看，这里对于一个非0向量，如果上述方程成立，那么矩阵A-λI必然是一个奇异矩阵，有det(A-λI)=0 ，问题得以解决。

Example

上例所求特征向量并非唯一，任意倍数的该向量都是特征向量，所以求解的只是一组基向量。

观察这个例子与上面的奇异矩阵的例子，不难发现这样的性质：

如果Ax=λx

那么(A+cI)x=Ax+cx=(λ+c)x

在求解特征值的过程中会涉及解关于λ的一元高次方程，它的解必然满足韦达定理，用矩阵的形式描述就是：

特征值之和等于矩阵的迹 tr (A)

特征值之积等于矩阵对应行列式的值 det A

注：迹tr(A)是矩阵对角线元素之和

最后再看一个旋转矩阵的例子

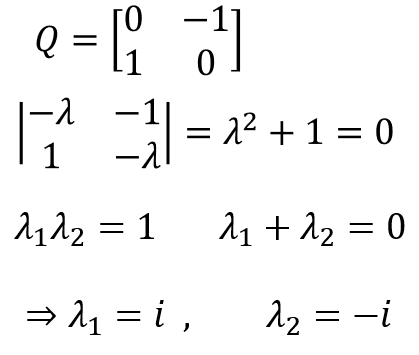
因此对于一个完全都是实数的矩阵，我们同样可能得到一组复数特征值，这个问题就像解实数方程有时会得到复数解一样。

根据高斯定理，一元n次方程有n个解

类比这里就是n阶矩阵有n个特征值