罗德里格斯(Rodrigues)旋转公式及其推导
罗德里格斯旋转公式及其推导
罗德里格斯(Rodrigues)旋转公式及其推导
三维空间旋转矩阵
计算机图形学中,三维空间下绕不同坐标轴的旋转矩阵如下(右手系逆时针):
绕X轴旋转:
R
x
=
[
1
0
0
0
c
o
s
θ
−
sin
θ
0
s
i
n
θ
cos
θ
]
(1)
R_x = \left[ \begin{matrix} \ 1 & 0 & 0 \\ \ 0 &cos \theta & -\sin \theta \\ \ 0 &sin \theta& \cos \theta \end{matrix} \right] \tag{1}
Rx=⎣⎡ 1 0 00cosθsinθ0−sinθcosθ⎦⎤(1)
绕Y轴旋转:
R
y
=
[
cos
θ
0
sin
θ
0
1
0
−
sin
θ
0
cos
θ
]
(2)
R_y= \left[ \begin{matrix} \cos \theta & 0 & \sin \theta \\ \ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{matrix} \right] \tag{2}
Ry=⎣⎡cosθ 0−sinθ010sinθ0cosθ⎦⎤(2)
绕Z轴旋转:
R
z
=
[
c
o
s
θ
−
sin
θ
0
s
i
n
θ
cos
θ
0
0
0
1
]
(3)
R_z = \left[ \begin{matrix} \ cos \theta & -\sin \theta & 0 \\ \ sin \theta& \cos \theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] \tag{3}
Rz=⎣⎡ cosθ sinθ0−sinθcosθ0001⎦⎤(3)
可以看到,这三个旋转矩阵,只有在三维空间下物体围绕某一特定坐标轴旋转的特殊情况下才能使用。从几何角度来讲,三维空间中任意一个旋转(绕任意轴),都可以分解为绕X轴,Y轴,Z轴旋转的复合。即对于任意旋转轴
n
⃗
\vec{n}
n,旋转角
θ
\theta
θ:
R
(
n
⃗
,
θ
)
=
R
(
x
⃗
,
θ
x
)
∗
R
(
y
⃗
,
θ
y
)
∗
R
(
z
⃗
,
θ
z
)
.
(4)
R(\vec{n},\theta) = R(\vec{x},\theta x) * R(\vec{y},\theta y) * R(\vec{z},\theta z)\,.\tag{4}
R(n,θ)=R(x,θx)∗R(y,θy)∗R(z,θz).(4)
然而,这样分解与矩阵运算的计算量显然是十分大的。
罗德里格斯旋转方程(Rodrigues)
罗德里格斯旋转公式,用于表示空间中任一向量
v
⃗
\vec{v}
v,沿任一旋转轴
k
⃗
\vec{k}
k, 旋转任一角度
θ
\theta
θ后,得到的结果:
v
⃗
r
o
t
=
v
⃗
cos
θ
+
(
1
−
cos
θ
)
(
k
⃗
⋅
v
⃗
)
⋅
k
⃗
+
sin
θ
∗
k
⃗
×
v
⃗
(5)
\vec{v}_{rot} = \vec{v} \cos\theta + (1-\cos\theta)(\vec{k} \cdot\ \vec{v})\cdot \vec{k} + \sin\theta *\vec{k} \times \vec{v} \tag{5}
vrot=vcosθ+(1−cosθ)(k⋅ v)⋅k+sinθ∗k×v(5)
这个式子还不是很直观,所以需要引入另外两个公式来再推导两步化简:
叉积矩阵
~~~~~~~
关于
a
⃗
×
b
⃗
\vec{a} \times \vec{b}
a×b ,有:
(
x
a
y
a
z
a
)
×
(
x
b
y
b
z
b
)
=
(
y
a
z
b
−
z
a
y
b
z
a
x
b
−
x
a
z
b
x
a
y
b
−
y
a
x
b
)
(6)
\begin{pmatrix} x_a \\y_a \\ z_a \end{pmatrix} \times \begin{pmatrix} x_b \\y_b \\ z_b \end{pmatrix}= \begin{pmatrix} y_az_b - z_ay_b \\z_ax_b - x_az_b \\ x_ay_b -y_ax_b \end{pmatrix}\tag{6}
⎝⎛xayaza⎠⎞×⎝⎛xbybzb⎠⎞=⎝⎛yazb−zaybzaxb−xazbxayb−yaxb⎠⎞(6)
~~~~~~~
可以写成矩阵形式:
(
y
a
z
b
−
z
a
y
b
z
a
x
b
−
x
a
z
b
x
a
y
b
−
y
a
x
b
)
=
(
0
−
z
a
y
a
z
a
0
−
x
a
−
y
a
x
a
0
)
⋅
(
x
b
y
b
z
b
)
(7)
\begin{pmatrix} y_az_b - z_ay_b \\z_ax_b - x_az_b \\ x_ay_b -y_ax_b \end{pmatrix} = \begin{pmatrix} 0&-z_a & y_a \\z_a &0&-x_a \\ -y_a &x_a &0 \end{pmatrix} \cdot \begin{pmatrix} x_b \\y_b \\ z_b \end{pmatrix}\tag{7}
⎝⎛yazb−zaybzaxb−xazbxayb−yaxb⎠⎞=⎝⎛0za−ya−za0xaya−xa0⎠⎞⋅⎝⎛xbybzb⎠⎞(7)
~~~~~~~
则可记
a
⃗
\vec{a}
a 的 " 叉积矩阵 " 为:
R
a
⃗
=
(
0
−
z
a
y
a
z
a
0
−
x
a
−
y
a
x
a
0
)
(8)
R_{\vec{a}} = \begin{pmatrix} 0&-z_a & y_a \\z_a &0&-x_a \\ -y_a &x_a &0 \end{pmatrix} \tag{8}
Ra=⎝⎛0za−ya−za0xaya−xa0⎠⎞(8)
~~~~~~~
对于任意向量
b
⃗
\vec{b}
b , 有 :
a
⃗
×
b
⃗
=
R
a
⃗
⋅
b
⃗
(9)
\vec{a} \times \vec{b} = R_{\vec{a}} \cdot \vec{b}\tag{9}
a×b=Ra⋅b(9)
拉格朗日公式(向量三重积展开)
~~~~~~~
对于三个向量
a
⃗
b
⃗
c
⃗
\vec{a} ~\vec{b} ~\vec{c}
a b c ,向量的三重积定义为:
a
⃗
×
(
b
⃗
×
c
⃗
)
\vec{a} \times (\vec{b} \times \vec{c})
a×(b×c)
~~~~~~~
值得注意的是,一般来说 :
a
⃗
×
(
b
⃗
×
c
⃗
)
≠
(
a
⃗
×
b
⃗
)
×
c
⃗
\vec{a} \times (\vec{b} \times \vec{c}) \neq(\vec{a} \times \vec{b}) \times \vec{c}
a×(b×c)=(a×b)×c
~~~~~~~
以下恒等式,称作三重积展开或拉格朗日公式,对于任意向量
a
⃗
、
b
⃗
、
c
⃗
\vec{a}、\vec{b}、\vec{c}
a、b、c 均成立 :
a
⃗
×
(
b
⃗
×
c
⃗
)
=
(
a
⃗
⋅
c
⃗
)
b
⃗
−
(
a
⃗
⋅
b
⃗
)
c
⃗
(10)
\vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c}) ~\vec{b} -(\vec{a} \cdot \vec{b}) ~\vec{c}\tag{10}
a×(b×c)=(a⋅c) b−(a⋅b) c(10)
罗德里格斯旋转方程推导
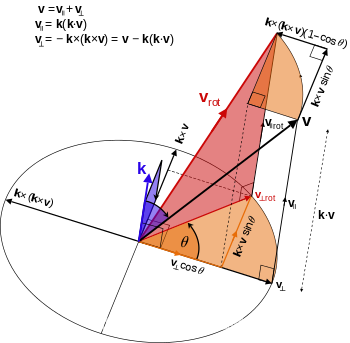
~~~~~~~
如上图所示,描述了一个空间中的向量
v
⃗
\vec{v}
v,沿旋转轴
k
⃗
\vec{k}
k(单位向量), 逆时针旋转了
θ
\theta
θ角度到
v
⃗
r
o
t
\vec{v}_{rot}
vrot的几何关系。
~~~~~~~
在
v
⃗
与
k
⃗
\vec{v} 与 \vec{k}
v与k组成的平面上,
v
⃗
\vec{v}
v可以分解为:与
k
⃗
\vec{k}
k垂直的分量
v
⊥
⃗
\vec{v_{\perp}}
v⊥和与
k
⃗
\vec{k}
k平行的分量
v
∥
⃗
\vec{v_{\parallel}}
v∥,有:
v
⃗
=
v
∥
⃗
+
v
⊥
⃗
v
⃗
r
o
t
=
v
⃗
r
o
t
∥
+
v
⃗
r
o
t
⊥
(11)
\vec{v} = \vec{v_{\parallel}} + \vec{v_{\perp}} \tag{11} ~~ \vec{v}_{rot} = \vec{v}_{rot\parallel} + \vec{v}_{rot\perp}
v=v∥+v⊥ vrot=vrot∥+vrot⊥(11)
~~~~~~~
其中,易得:
v
∥
⃗
=
(
v
⃗
⋅
k
⃗
)
∗
k
⃗
(12)
\vec{v_{\parallel}} = (\vec{v} \cdot \vec{k}) * \vec{k}\tag{12}
v∥=(v⋅k)∗k(12)
~~~~~~~
则,由(11)式:
v
⊥
⃗
=
v
⃗
−
v
∥
⃗
=
v
⃗
−
(
v
⃗
⋅
k
⃗
)
∗
k
⃗
(13)
\vec{v_{\perp}} = \vec{v} - \vec{v_{\parallel}} = \vec{v} - (\vec{v} \cdot \vec{k}) * \vec{k}\tag{13}
v⊥=v−v∥=v−(v⋅k)∗k(13)
~~~~~~~
由 (10)式拉格朗日公式:
v
⃗
−
(
v
⃗
⋅
k
⃗
)
∗
k
⃗
=
(
k
⃗
⋅
k
⃗
)
∗
v
⃗
−
(
k
⃗
⋅
v
⃗
)
∗
k
⃗
=
k
⃗
×
(
v
⃗
×
k
)
⃗
(14)
\vec{v} - (\vec{v} \cdot \vec{k}) * \vec{k} = (\vec{k} \cdot \vec{k}) *\vec{v} - (\vec{k} \cdot \vec{v}) * \vec{k} = \vec{k} \times(\vec{v}\times \vec{k)}\tag{14}
v−(v⋅k)∗k=(k⋅k)∗v−(k⋅v)∗k=k×(v×k)(14)
~~~~~~~
则:
v
⊥
⃗
=
k
⃗
×
(
v
⃗
×
k
)
⃗
=
−
k
⃗
×
(
k
⃗
×
v
)
⃗
(15)
\vec{v_{\perp}} = \vec{k} \times(\vec{v}\times \vec{k)} = -\vec{k} \times(\vec{k}\times \vec{v)}\tag{15}
v⊥=k×(v×k)=−k×(k×v)(15)
~~~~~~~
根据几何关系,平行于旋转轴的分量在旋转时不会改变其幅度和方向,因此有:
v
⃗
r
o
t
∥
=
v
⃗
∥
(16)
\vec{v}_{rot\parallel} = \vec{v}_{\parallel} \tag{16}
vrot∥=v∥(16)
~~~~~~~
解旋转后的垂直分量,由图中的几何关系可得
v
⃗
r
o
t
⊥
\vec{v}_{rot\perp}
vrot⊥可以分解为
k
⃗
×
v
⃗
\vec{k} \times \vec{v}
k×v和
v
⃗
⊥
\vec{v}_{\perp}
v⊥方向上两个分量相加,即
v
⃗
r
o
t
⊥
=
v
⃗
r
o
t
⊥
⋅
k
⃗
×
v
⃗
∣
k
⃗
×
v
⃗
∣
+
v
⃗
r
o
t
⊥
⋅
v
⃗
⊥
∣
v
⃗
⊥
∣
=
sin
θ
∗
(
k
⃗
×
v
⃗
)
+
cos
θ
∗
v
⃗
⊥
(17)
\begin{aligned} \vec{v}_{rot\perp} = \vec{v}_{rot\perp} \cdot \frac{\vec{k} \times \vec{v}}{ \vert \vec{k} \times \vec{v} \vert}+ \vec{v}_{rot\perp} \cdot \frac{\vec{v}_{\perp}}{\vert\vec{v}_{\perp\vert}} = \sin\theta * (\vec{k} \times \vec{v}) + \cos\theta * \vec{v}_{\perp} \tag{17} \end{aligned}
vrot⊥=vrot⊥⋅∣k×v∣k×v+vrot⊥⋅∣v⊥∣v⊥=sinθ∗(k×v)+cosθ∗v⊥(17)
~~~~~~~
将(12)(16)(17)式代入,有:
v
⃗
r
o
t
=
v
⃗
∥
+
cos
θ
∗
(
v
⃗
−
v
⃗
∥
)
+
sin
θ
∗
(
k
⃗
×
v
⃗
)
=
cos
θ
v
⃗
+
(
1
−
cos
θ
)
v
⃗
∥
+
sin
θ
(
k
⃗
×
v
⃗
)
=
v
⃗
cos
θ
+
(
1
−
cos
θ
)
(
k
⃗
⋅
v
⃗
)
⋅
k
⃗
+
sin
θ
∗
k
⃗
×
v
⃗
=
式
5
\begin{aligned} \vec{v}_{rot}&= \vec{v}_{\parallel} + \cos\theta * (\vec{v} - \vec{v}_{\parallel}) + \sin\theta * (\vec{k} \times \vec{v})\\&=\cos\theta\vec{v} + (1 - \cos\theta)\vec{v}_\parallel + \sin\theta(\vec{k} \times \vec{v})\\&=\vec{v} \cos\theta + (1-\cos\theta)(\vec{k} \cdot\ \vec{v})\cdot \vec{k} + \sin\theta *\vec{k} \times \vec{v}&=式5 \end{aligned}
vrot=v∥+cosθ∗(v−v∥)+sinθ∗(k×v)=cosθv+(1−cosθ)v∥+sinθ(k×v)=vcosθ+(1−cosθ)(k⋅ v)⋅k+sinθ∗k×v=式5
~~~~~~~
此式还可继续化简,变成矩阵形式:
v
⃗
r
o
t
=
v
⃗
cos
θ
+
(
1
−
cos
θ
)
(
k
⃗
⋅
v
⃗
)
⋅
k
⃗
+
sin
θ
∗
k
⃗
×
v
⃗
=
v
⃗
−
v
⃗
+
v
⃗
cos
θ
+
(
1
−
cos
θ
)
(
k
⃗
⋅
v
⃗
)
⋅
k
⃗
+
sin
θ
∗
k
⃗
×
v
⃗
=
v
⃗
−
(
1
−
cos
θ
)
v
⃗
+
(
1
−
cos
θ
)
(
k
⃗
⋅
v
⃗
)
⋅
k
⃗
+
sin
θ
∗
k
⃗
×
v
⃗
=
v
⃗
+
(
1
−
cos
θ
)
(
(
k
⃗
⋅
v
⃗
)
k
⃗
−
(
k
⃗
⋅
k
⃗
)
v
⃗
)
+
sin
θ
∗
k
⃗
×
v
⃗
=
v
⃗
+
sin
θ
k
⃗
×
v
⃗
+
(
1
−
cos
θ
)
k
⃗
×
(
k
⃗
×
v
⃗
)
\begin{aligned} \vec{v}_{rot} &= \vec{v} \cos\theta + (1-\cos\theta)(\vec{k} \cdot\ \vec{v})\cdot \vec{k} + \sin\theta *\vec{k} \times \vec{v} \\&= \vec{v} - \vec{v} + \vec{v} \cos\theta + (1-\cos\theta)(\vec{k} \cdot\ \vec{v})\cdot \vec{k} + \sin\theta *\vec{k} \times \vec{v} \\&= \vec{v} - (1-\cos\theta)\vec{v} +(1-\cos\theta)(\vec{k} \cdot\ \vec{v})\cdot \vec{k} + \sin\theta *\vec{k} \times \vec{v}\\&=\vec{v} + (1-\cos\theta)((\vec{k}\cdot\vec{v})\vec{k} - (\vec{k}\cdot\vec{k})\vec{v}) + \sin\theta *\vec{k} \times \vec{v} \\&=\vec{v}+\sin\theta\vec{k}\times\vec{v}+ (1-\cos\theta)\vec{k}\times(\vec{k}\times\vec{v}) \end{aligned}
vrot=vcosθ+(1−cosθ)(k⋅ v)⋅k+sinθ∗k×v=v−v+vcosθ+(1−cosθ)(k⋅ v)⋅k+sinθ∗k×v=v−(1−cosθ)v+(1−cosθ)(k⋅ v)⋅k+sinθ∗k×v=v+(1−cosθ)((k⋅v)k−(k⋅k)v)+sinθ∗k×v=v+sinθk×v+(1−cosθ)k×(k×v)
~~~~~~~
设
k
⃗
\vec{k}
k的叉积矩阵为
R
k
⃗
R_{\vec{k}}
Rk,有:
v
⃗
r
o
t
=
v
⃗
+
sin
θ
R
k
⃗
∗
v
⃗
+
(
1
−
cos
θ
)
R
k
⃗
∗
R
k
⃗
∗
v
⃗
=
(
I
+
sin
θ
R
k
⃗
+
(
1
−
cos
θ
)
R
k
⃗
2
)
∗
v
⃗
=
M
v
⃗
\begin{aligned} \vec{v}_{rot} &= \vec{v} + \sin\theta R_{\vec{k}} * \vec{v} + (1-\cos\theta) R_{\vec{k}} *R_{\vec{k}} * \vec{v} \\&=(I + \sin\theta R_{\vec{k}} + (1-\cos\theta) R_{\vec{k}}^2) * \vec{v}\\&=M\vec{v} \end{aligned}
vrot=v+sinθRk∗v+(1−cosθ)Rk∗Rk∗v=(I+sinθRk+(1−cosθ)Rk2)∗v=Mv
~~~~~~~
其中:
M
=
I
+
sin
θ
R
k
⃗
+
(
1
−
cos
θ
)
R
k
⃗
2
M = I + \sin\theta R_{\vec{k}} + (1-\cos\theta) R_{\vec{k}}^2
M=I+sinθRk+(1−cosθ)Rk2
~~~~~~~
为三维空间中任意向量绕轴
k
⃗
\vec{k}
k逆时针旋转
θ
\theta
θ角度的旋转矩阵。