矩阵范数计算例题_数值计算方法·目录和第一部分
目录
- 第一部分——误差和范数
- 第一章(误差、有效数字、稳定性、范数、算子范数、谱和特殊矩阵)
- 第二部分——矩阵和线性方程组
脑洞的窗:数值计算方法·第二部分·第二章zhuanlan.zhihu.com
脑洞的窗:数值计算方法·第二部分·第三和第四章zhuanlan.zhihu.com
- 第三部分——非线性方程、非线性函数、积分值和微分方程
脑洞的窗:数值计算方法·第三部分zhuanlan.zhihu.com
第一部分·第一章·误差和有效数字
设
为精确值,
为
的一个近似值:
误差
,误差界
,相对误差
,相对误差界

把
的形式,然后计算
,
就是有效数字(正数,如果低于0,即无有效数字)

四舍五入的数可以直接数有效数字。一般来说,绝对误差与小数位数有关,相对误差与有效数字位数有关
另有以下定理,证明见最后一句:

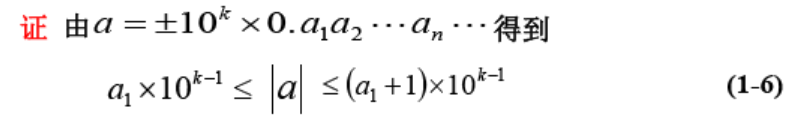
函数的绝对误差
,相对误差同理,多元函数偏导(代入a)×分量误差求和
四则运算:



计算中避免小数作除数和两个相近的数相减,避免有效位数损失,减少运算次数
稳定性作了解,主要是误差是否放大:

秦九韶算法:
从里往外算
范数和算子范数
满足以下定义:

加权的向量范数先权值矩阵×向量,再求解即可。
常用向量范数定义如下:
常用矩阵范数定义如下:

向量范数具有等价性,对均为
维的向量范数
和
,总能找到
与向量无关的正数
,使


(∞≤2≤1)
矩阵范数M与向量范数V相容,只要对任意矩阵和向量成立即可。
算子范数定义:
,它是
从属于向量范数V的,只要证明了这个式子,即可说明它是一种算子范数(不必证非负性、齐次性等)。
最常用的算子范数(分别从属于对应的向量范数):
(从矩阵的1,2,∞范数能导出对应向量的)
对任何算子范数,都有,所以m1范数和F范数都不是算子范数。
矩阵范数和向量范数必定可以找到相容者(
并不是说所有的矩阵和向量范数都相容),并且不是一一对应的关系。

矩阵的谱和特殊矩阵
方阵的谱
是特征值的集合,谱半径是特征值
的模里最大的那一个(思考:谱半径为什么不能作范数?)。
①可证明都是复对称(对称之后各元素取
共轭)半正定矩阵:

酉矩阵
,有
:
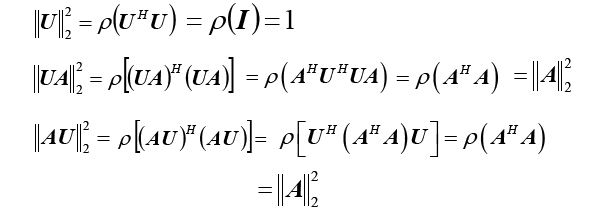
矩阵的谱半径不大于
任意一种范数,但只要任意加一个常数,总不小于
一种算子范数(这个算子范数和矩阵及常数都有关)


以下定理作了解:

版权声明:本文为weixin_32027779原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。