正交基函数

SH光照论文需要知道基函数（basis functions）知识。基函数就是小片的信号，可以被缩放、组合来产生原函数的近似，计算多少基函数需要被加到结果中的过程被称为投影（projection）。通过基函数估计原函数，需要找一个标量值，表示f(x)与Bi(x)的相似度，计算这个值，需要再f的全域内计算f(x)Bi(x)积分。

对所有得基函数，进行这个投影的过程，我们得到一个近似系数向量。

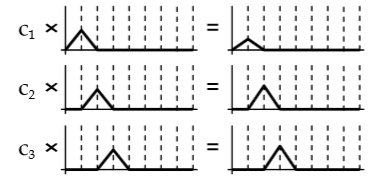
然后将结果累加，得到最后的估计函数。

在例子中，使用了一系列 的线性基函数（linear basis functions），使我们的到了输入函数得分段性近似（piecewise linear approximation）。存在许多可供我们使用的基函数，但是我们最感兴趣的一组基函数被数学家称为正交多项式（orthogonal polynomials）。

正交多项式是具有特别性质的多项式--当你对任意两个这种多项式的乘积做积分时，如果这两个多项式是一样 的，积分结果为常量，如果这两个多项式不同时，积分结果为0.

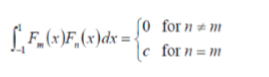
 我们可以进行更为严格的限制，如果我们要求任意两个多项式乘积的积分的结果为0或1，那么满足这个要求的字多相识集我们称为规范正交基函数（orthonormal basis functions）。直观上讲，这些函数占有相同的作用域，但是两者的影响力并不“重叠”，这个效果与将傅里叶变换分解为子分量正弦波（component sine waves）的 道理一样。

这种多项式常常是以研究它的数学家的名字来命名的，如切比雪夫，亚隔壁和艾尔米特。最感兴趣的勒让德多项式（Legendre polynomials），尤其是伴随勒让德多项式（Associalted Legendre Polynomials ）。用P表示，伴随勒让德多项式有两个参数l和m。两者的域都在[-1,1]之间，返回值为实数。

这两个参数l和m将这一组的多项式分成不同函数波段（band），参数l，就是波段索引（band index），其值为从0

开始的所有正整数，而m的值就是在域[0,l]内。在每一个波段内，多项式是关于一个常量正交得，而在不同波段间，多项式是关于另一个常量正交得，我们可以用一个三角形的图来显示每个波段函数，对n波段近似我们就得到了n（n+1）个系数。

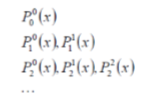
递归定义三条规则:

1.

2.

3.