信噪比与雷达探测距离之间关系

大大源码 • 2023年3月29日 pm10:36 • 其他

根据信噪比增益推导雷达的距离推远范围

根据雷达的基本工作原理推导雷达方程：

设雷达的发射机功率为

P_{t}

$P_{t}$ ，当用各向均匀的天线向外发射，距离雷达

$R$ 远处的任一点的功率密度

′

S_{1}^{'}

$S_{1}^{^{'}}$ 等于功率被理想球面

4\pi{R}^{2}

$4 π R^{2}$ 所除，即

\begin{equation} S_{1}= \frac{P_{t}}{4\pi{R^{2}}} \end{equation}

$S_{1} = \frac{P _{t}}{4 π R ^{2}}$

实际的雷达工作时将发射功率集中在某些方向上。天线增益G用来表示对于各向同性的天线，实际天线在辐射方向上的功率增加的倍数。因此，当天线增益为G时，距离雷达目标所照射的功率密度为：

\begin{equation} S_{1}=\frac{P_{t}G}{4\pi{R}^{2}} \end{equation}

$S_{1} = \frac{P _{t} G}{4 π R ^{2}}$

雷达辐射出去的功率经过目标接收面积

\sigma

$σ$ 反射再次辐射到雷达处功率表示为：

\begin{equation} S_{2}=S_{1}\frac{\sigma}{4\pi{R^{2}}} \end{equation}

$S_{2} = S_{1} \frac{σ}{4 π R ^{2}}$

假设雷达的接收天线的有效面积为

A_{e}

$A_{e}$ ,则雷达收到的回波功率

P_{r}

$P_{r}$ 为：

\begin{equation} P_{r}=A_{e}S_{2}=\frac{P_{t}GA_{e}\sigma}{4\pi{R^{4}}} \end{equation}

$P_{r} = A_{e} S_{2} = \frac{P _{t} G A _{e} σ}{4 π R ^{4}}$

接收到的回波功率等于最小可检测到信号的功率(

P_{min}

$P_{min}$ )的时候，推出雷达最大可探测距离为

R_{max}

$R_{ma x}$ 为：

(

)

\begin{equation} R_{max}=(\frac{P_{t}GA_{e}\sigma}{(4\pi)^{2}P_{min}})^{\frac{1}{4}} \end{equation}

$R_{ma x} = (\frac{P _{t} G A _{e} σ}{( 4 π ) ^{2} P _{min}})^{\frac{1}{4}}$

我们现在因为项目需求，需要知道在检测概率

0.8

P_{d}=0.8

$P_{d} = 0.8$ 的时候根据SNR的增益推导出距离的推远范围：

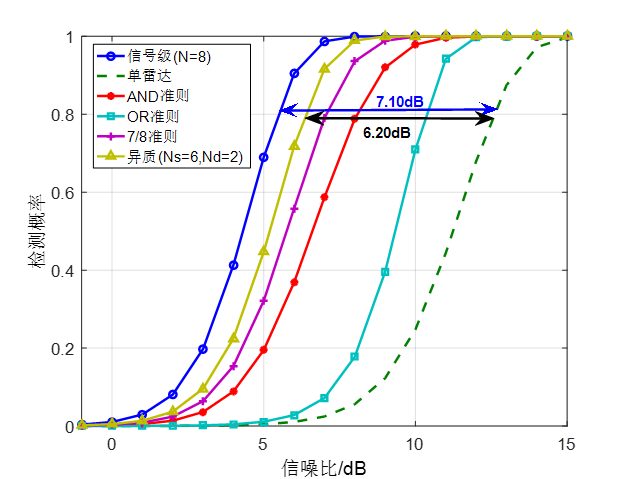
在这里插入图片描述

根据雷达方程推导出

$R$ 和信噪比之间的关系

步骤一：根据雷达方程可知：

(

)

(

)

\begin{equation} R_{1}=(\frac{P_{t}GA_{e}\sigma_1}{(4\pi)^{2}P_{min}})^{\frac{1}{4}}\ R_{2}=(\frac{P_{t}GA_{e}\sigma_2}{(4\pi)^{2}P_{min}})^{\frac{1}{4}} \end{equation}

$R_{1} = (\frac{P _{t} G A _{e} σ _{1}}{( 4 π ) ^{2} P _{min}})^{\frac{1}{4}} R_{2} = (\frac{P _{t} G A _{e} σ _{2}}{( 4 π ) ^{2} P _{min}})^{\frac{1}{4}}$

将方程相比(相一样的参数相消),其中 $P_1 P_2$ 为接收功率比：

$KaTeX parse error: {equation} can be used only in display mode.$

根据信噪比的定义：

\begin{equation} SNR = 10lg\frac{P_s}{P_n} \end{equation}

$SNR = 10 l g \frac{P _{s}}{P _{n}}$

△

\begin{equation} lg10^{\triangle SNR} = 10lg\frac{P_s}{P_n} \end{equation}

$l g 1 0^{△ SNR} = 10 l g \frac{P _{s}}{P _{n}}$

△

(

)

\begin{equation} 10^{\triangle SNR} = (\frac{P_s}{P_n})^{10} \end{equation}

$1 0^{△ SNR} = (\frac{P _{s}}{P _{n}})^{10}$

△

\begin{equation} \frac{P_s}{P_n}=10^{\frac{\triangle SNR}{10}} \end{equation}

$\frac{P _{s}}{P _{n}} = 1 0^{\frac{△ SNR}{10}}$

将功率用信噪比增益表示出来，带入距离比的式子得到：

△

\begin{equation} \frac{R_1}{R_2}=10^{\frac{\triangle SNR}{40}} \end{equation}

$\frac{R _{1}}{R _{2}} = 1 0^{\frac{△ SNR}{40}}$

根据图中在信噪比增益为7.1dB可以知道在这种条件下距离推远为 $10^{\frac{7.1}{40}}=1.5049$ ,在原来的距离基础上推远了50.49%.

原文链接：https://blog.csdn.net/qq_42961235/article/details/127464790

THE END

大大搜源码

搜索内容

信噪比与雷达探测距离之间关系

根据信噪比增益推导雷达的距离推远范围