11QR分解

大大源码 • 2023年3月22日 pm10:31 • 其他

QR分解

1.定义
2.定理
3.求QR分解的办法
- 3.1Gives变换（利用Gives变换的 $Tx=|x|e_1$ ）
- 3.2Householder变换（利用 $H x = ∣ x ∣ z$ ）

1.定义

矩阵A可以化为正交（酉）矩阵Q和上三角矩阵R的乘积，即

A=QR

$A = Q R$ ，则称上式为矩阵的

$Q R$ 分解

2.定理

若

$A$ 是一个

$n$ 阶非奇异矩阵，则存在正交（酉）矩阵

$Q$ 和上三角矩阵

$R$ 使得

A=QR

$A = Q R$ ，且除去相差一个对角元素绝对值全为1的对角因子外，上述分解唯一。
回顾一下施密特正交化的过程
在这里插入图片描述
可以得到施密特正交化的矩阵为

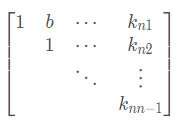
证明：
设

[

]

A=[a_1,a_2...a_n]

$A = [a_{1}, a_{2} . . . a_{n}]$ ,且

a_1,a_2,...a_n

$a_{1}, a_{2}, . . . a_{n}$ 线性无关。应用施密特正交化的办法可以得到

[

⋯

]

[

⋯

]

[

⋯

⋱

⋮

−

]

\left[ \begin{matrix} a_1 & a_2 & \cdots & a_n \end{matrix} \right]=\left[ \begin{matrix} b_1 & b_2 & \cdots & b_n \end{matrix} \right]\left[ \begin{matrix} 1 & b & \cdots & k_{n1} \\ & 1 & \cdots & k_{n2} \\ & & \ddots & \vdots \\ & & & k_{nn-1} \end{matrix} \right]

$[a_{1} a_{2} \dots a_{n}] = [b_{1} b_{2} \dots b_{n}] ⎣ ⎢ ⎢ ⎢ ⎡ 1 b 1 \dots \dots ⋱ k_{n 1} k_{n 2} ⋮ k_{n n - 1} ⎦ ⎥ ⎥ ⎥ ⎤$ 对其单位化可得

[

⋯

]

[

⋯

]

[

∣

⋱

∣

]

[

⋯

⋱

⋮

−

]

\left[ \begin{matrix} a_1 & a_2 & \cdots & a_n \end{matrix} \right]=\left[ \begin{matrix} q_1 & q_2 & \cdots & q_n \end{matrix} \right]\left[ \begin{matrix} |b_1| & & & \\ & |b_2| & & \\ & & \ddots & \\ & & & |b_n| \end{matrix} \right]\left[ \begin{matrix} 1 & b & \cdots & k_{n1} \\ & 1 & \cdots & k_{n2} \\ & & \ddots & \vdots \\ & & & k_{nn-1} \end{matrix} \right]=QR

$[a_{1} a_{2} \dots a_{n}] = [q_{1} q_{2} \dots q_{n}] ⎣ ⎢ ⎢ ⎡ ∣ b_{1} ∣ ∣ b_{2} ∣ ⋱ ∣ b_{n} ∣ ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ 1 b 1 \dots \dots ⋱ k_{n 1} k_{n 2} ⋮ k_{n n - 1} ⎦ ⎥ ⎥ ⎥ ⎤ = Q R$ 接下来我们证明其唯一性：
假设有两个QR分解

A=QR=Q_1R_1

$A = Q R = Q_{1} R_{1}$

−

Q=Q_1R_1R^{-1}=Q_1D

$Q = Q_{1} R_{1} R^{- 1} = Q_{1} D$ 因为

R_1,R

$R_{1}, R$ 都为上三角矩阵，而上三角矩阵的逆为上三角矩阵，上三角矩阵成上三角矩阵还是上三角矩阵因此

$D$ 是上三角矩阵。又

I=Q^HQ=D^HQ_1^HQ_1D=D^HD

$I = Q^{H} Q = D^{H} Q_{1}^{H} Q_{1} D = D^{H} D$ 所以

$D$ 是酉矩阵。所以，

$D$ 只能是对角元素绝对值全为1的对角阵

3.求QR分解的办法

3.1Gives变换（利用Gives变换的 $Tx=|x|e_1$ ）

例题：利用

变

换

Givens变换

$G i v e n s 变换$ 求

[

]

A=\left[ \begin{matrix} 2 & 2& 1 \\ 0 & 2& 2\\ 2 & 1 & 2 \end{matrix} \right]

$A = ⎣ ⎡ 202221122 ⎦ ⎤$ 的

分

解

QR分解

$Q R 分解$ （正交矩阵的转置就是其逆）
解：首先对第一列进行Givens变换，有

[

−

]

T_{13}=\left[ \begin{matrix} c & 0& s \\ 0 & 1& 0\\ -s & 0 & c \end{matrix} \right] ,c=\frac{a_{11}}{\sqrt{a_{11}^2+a_{31}^2}}=\frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2}},s=\frac{a_{31}}{\sqrt{a_{11}^2+a_{31}^2}}=\frac{1}{\sqrt{2}}

$T_{13} = ⎣ ⎡ c 0 - s 010 s 0 c ⎦ ⎤, c = \frac{a _{11}}{a _{11}^{2} + a _{31}^{2}} = \frac{2}{2 2} = \frac{1}{2}, s = \frac{a _{31}}{a _{11}^{2} + a _{31}^{2}} = \frac{1}{2}$ 所以可得

[

−

]

[

−

]

(

)

[

−

]

T_1=\left[ \begin{matrix} \frac{1}{\sqrt{2}} & 0& \frac{1}{\sqrt{2}} \\ 0 & 1& 0\\ -\frac{1}{\sqrt{2}} & 0& \frac{1}{\sqrt{2}} \end{matrix} \right] ,T_1A=\left[ \begin{matrix} 2\sqrt{2} & \frac{3}{\sqrt{2}}&\frac{3}{\sqrt{2}} \\ 0 & 2& 2\\ 0 & -\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \end{matrix} \right],A^{(1)}=\left[ \begin{matrix} 2& 2\\ -\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \end{matrix} \right]

$T_{1} = ⎣ ⎡ \frac{1}{2} 0 - \frac{1}{2} 010 \frac{1}{2} 0 \frac{1}{2} ⎦ ⎤, T_{1} A = ⎣ ⎢ ⎡ 2200 \frac{3}{2} 2 - \frac{1}{2} \frac{3}{2} 2 \frac{1}{2} ⎦ ⎥ ⎤, A^{(1)} = [2 - \frac{1}{2} 2 \frac{1}{2}]$ 对

(

)

A^{(1)}

$A^{(1)}$ 再进行Givens变换，可以得到

[

−

]

−

T_{12}=\left[ \begin{matrix} c & s \\ -s & c \end{matrix} \right],c=\frac{2\sqrt{2}}{3},s=-\frac{1}{3}

$T_{12} = [c - s s c], c = \frac{2 2}{3}, s = - \frac{1}{3}$ 所以可得

[

−

]

(

)

[

]

T2=\left[ \begin{matrix} \frac{2\sqrt{2}}{3} & -\frac{1}{3} \\ \frac{1}{3} & \frac{2\sqrt{2}}{3} \end{matrix} \right],T_2A^{(1)}=\left[ \begin{matrix} \frac{2\sqrt{2}}{3} & \frac{7\sqrt{2}}{6} \\ 0 & \frac{4}{3} \end{matrix} \right],

$T 2 = [\frac{2 2}{3} \frac{1}{3} - \frac{1}{3} \frac{2 2}{3}], T_{2} A^{(1)} = [\frac{2 2}{3} 0 \frac{7 2}{6} \frac{4}{3}],$ 综上可得，

[

]

[

]

[

−

]

R=\left[ \begin{matrix} 2\sqrt{2} & \frac{3}{\sqrt{2}}&\frac{3}{\sqrt{2}} \\ 0 & \frac{2\sqrt{2}}{3} & \frac{7\sqrt{2}}{6}\\ 0 & 0 & \frac{4}{3} \end{matrix} \right],Q=\left[\left[ \begin{matrix} 1 & 0 \\ 0& T2 \end{matrix} \right]T_1\right]^T=\left[ \begin{matrix} \frac{1}{\sqrt{2}} & \frac{1}{3\sqrt{2}}&-\frac{2}{3} \\ 0 & \frac{2\sqrt{2}}{3} & \frac{7\sqrt{2}}{6}\\ \frac{1}{\sqrt{2}} & -\frac{1}{3\sqrt{2}}& \frac{2}{3} \end{matrix} \right]

$R = ⎣ ⎢ ⎡ 2200 \frac{3}{2} \frac{2 2}{3} 0 \frac{3}{2} \frac{7 2}{6} \frac{4}{3} ⎦ ⎥ ⎤, Q = [[10 0 T 2] T_{1}]^{T} = ⎣ ⎢ ⎡ \frac{1}{2} 0 \frac{1}{2} \frac{1}{3 2} \frac{2 2}{3} - \frac{1}{3 2} - \frac{2}{3} \frac{7 2}{6} \frac{2}{3} ⎦ ⎥ ⎤$

3.2Householder变换（利用 $H x = ∣ x ∣ z$ ）

将

$z$ 矩阵设为e矩阵，u=

−

∣

−

∣

\frac{x-|x|z}{|x-|x|z|}

$\frac{x - ∣ x ∣ z}{∣ x - ∣ x ∣ z ∣}$
利用Householder求

[

]

A=\left[ \begin{matrix} 0 & 4& 1 \\ 1 & 1& 1\\ 0 & 3 & 2 \end{matrix} \right]

$A = ⎣ ⎡ 010413112 ⎦ ⎤$ 的

$Q R$ 分解
解：首先对第一列使用Householder变换，可以得到

−

∣

−

∣

−

∣

[

−

]

[

−

]

H=I-2uu^T,|x-|x|e_1|=\sqrt{2},x-|x|e_1=\left[ \begin{matrix} -1\\ 1 \\ 0 \end{matrix} \right],u=\frac{1}{\sqrt{2}}\left[ \begin{matrix} -1\\ 1 \\ 0 \end{matrix} \right]

$H = I - 2 u u^{T}, ∣ x - ∣ x ∣ e_{1} ∣ = 2, x - ∣ x ∣ e_{1} = ⎣ ⎡ - 1 10 ⎦ ⎤, u = \frac{1}{2} ⎣ ⎡ - 1 10 ⎦ ⎤$

[

−

]

[

−

]

[

−

]

2uu^T=\frac{1}{\sqrt{2}}\left[ \begin{matrix} -1\\ 1 \\ 0 \end{matrix} \right]\frac{1}{\sqrt{2}}\left[ \begin{matrix} -1 &1 & 0 \end{matrix} \right]=\frac{1}{2}\left[ \begin{matrix} 1&-1&0\\ -1&1&0 \\ 0&0&0 \end{matrix} \right]

$2 u u^{T} = \frac{1}{2} ⎣ ⎡ - 1 10 ⎦ ⎤ \frac{1}{2} [- 1 10] = \frac{1}{2} ⎣ ⎡ 1 - 1 0 - 1 10 000 ⎦ ⎤$