Matlab 小波变换降噪

小波变换是一种类似于傅里叶变换的信号处理方法，本篇主要探索其在 matlab 中如何应用降噪。

首先我们新建wavelet_demo.m文件

清除之前的代码：

clc;
clear;

加载数据集：

% 加载数据集
load leleccum;
% 设置窗口标题
figure('Name',"Wavelet Reconstruction");

首先显示原来的信号：

subplot(3,1,1)
plot(leleccum);
title('Original Signal')

使用哈尔小波基：

% 用哈尔小波基 进行三层小波分解
% 由分解得到粗尺度近似系数和细节系数。
% c 代表小波分解向量,需要根据向量l来进行分解
% l 代表Bookkeeping vector，用其来对c的系数进行分解
[c,l] = wavedec(leleccum,3,'haar');

得到分解分量：

% appcoef 是一维近似系数
approx = appcoef(c,l,'haar');

% detcoef 是一维细节系数
[cd1,cd2,cd3] = detcoef(c,l,[1 2 3]);

重置部分分量：

cdd1=zeros(size(cd1));
cdd2=zeros(size(cd2)); 
% 组合各个分量
com1=[approx cd3 cdd2 cdd1];
aa1=waverec(com1,l,'haar');

画出经过一次的离散小波变换图像：

title('DWT Once Signal')
subplot(3,1,2)
plot(aa1)

同理，我们再进行一次降噪：

[c,l] = wavedec(aa1,3,'haar');
approx = appcoef(c,l,'haar');
[cd1,cd2,cd3] = detcoef(c,l,[1 2 3]);
cdd3=zeros(size(cd3));
com1=[approx cdd3 cd2 cd1];
aa1=waverec(com1,l,'haar');
title('DWT Twice Signal');
subplot(3,1,3)
plot(aa1)

降噪的效果如下：

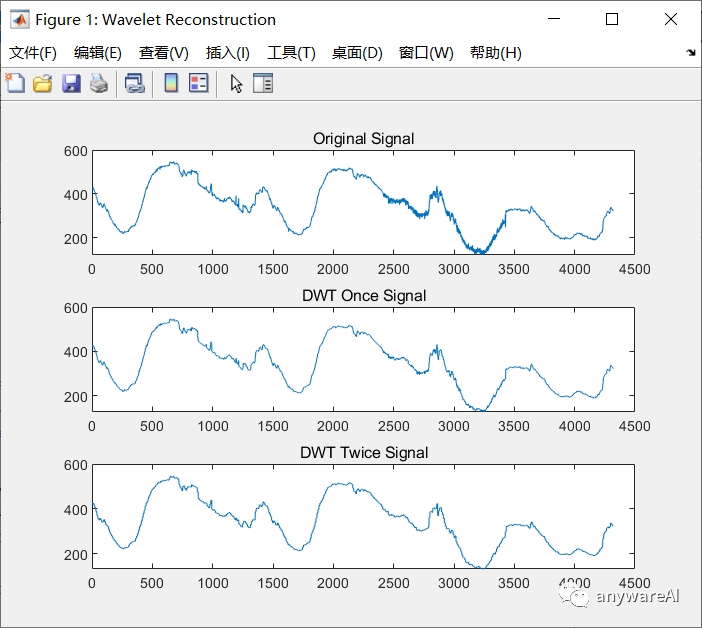
当然，你也可以稍微修改一下以查看各个分量的信息：

figure(2);
subplot(4,1,1)
plot(approx)
title('Approximation Coefficients')
subplot(4,1,2)
plot(cd3)
title('Level 3 Detail Coefficients')
subplot(4,1,3)
plot(cd2)
title('Level 2 Detail Coefficients')
subplot(4,1,4)
plot(cd1)
title('Level 1 Detail Coefficients')

有时候我们可能要用到高通或者低通滤波器：

% LOD-分解低通滤波器
% HiD—分解高通滤波器
% LoR—重构低通滤波器
% HiR—重构高通滤波器
% [LoD,HiD,LoR,HiR] = wfilters('haar');