定义1：如果V(G)={v1，v2,v3,...,vp};则称非负整数序列(d(v1),d(v2),d(v3),...,d(vp))为图G的度序列.

(定义中的图指广义的图,含有多重边或环).

定义2：简单图的度序列成为图序列.

以下是图论书上的定理及推论:

定理1（握手定理）：对于每个图G=(V,E),均有∑d(v)(v属于V)=2*q(G),(q(G)为图的边数).

推论1：任何图中,奇点的个数为偶数.

推论2：非负整数序列(d1,d2,...,dp)是某个图的度序列,则所有度之和∑(di)(1<=i<=n)是偶数.

可简单图化的判定（Havel定理）：

把序列排成不增序，即d1>=d2>=……>=dn，则d可简单图化当且仅当d’={d2-1，d3-1，……d(d1+1)-1， d(d1+2)，d(d1+3)，……dn}可简单图化。简单的说，把d排序后，找出度最大的点（设度为d1），把它与度次大的d1个点之间连边，然后这个点就可以不管了，一直继续这个过程，直到建出完整的图，或出现负度等明显不合理的情况。

证明请看：http://journals.cambridge.org/download.php?file=%2FBAZ%2FBAZ33_01%2FS0004972700002872a.pdf&code=2cca4625499f37e69a01ec5fab104dcd

其证明其实很简单，思想就是图的子图也一定是图，拆一个点后，它依然是图，直到拆完，图才消失。和证明正定矩阵和数学归纳法很像。

Havel算法的思想简单的说如下：

(1)对序列从大到小进行排序。

(2)设最大的度数为t,把最大的度数置0,然后把最大度数后(不包括自己)的t个度数分别减1(意思就是把度数最大的点与后几个点进行连接)

(3)如果序列中出现了负数,证明无法构成。如果序列全部变为0,证明能构成,跳出循环.前两点不出现，就跳回第一步！

这里举个例子：

假设一个度序列（已经是非递增顺序排序）
3,3,3,3,2

1.由于最大的是3，则从第2个开始，后面3个的值都要减去1，同时第1个值置0，即得0,2,2,2,2

2.重新排序后为2,2,2,2,0。最大的为2，则从第2个开始，后面2个的值都要减去1，同时第1个值置0，即0,1,1,2,0

3.重新排序后为2,1,1,0,0。最大的为2，则从2个开始，后面的2个值都要减去1，同时第1个值置0，即0,0,0,0,0，全部的值已经为0，即可以成图

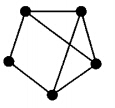
实际上，我们可以绘这样图

又假设一个度序列（已经是非递增顺序排序）4,4,3,2,1

按照上面的方法，可以得到如下序列

0,3,2,1,0-----3,2,1,0,0

0,1,0,-1,0，出现负数，则不能成图

C程序代码如下：

int cmp(const void *a, const void *b)
{
     return(*(int *)b-*(int *)a);//非递增排序
}

bool havel(int p[],int len)
{
	qsort(p,len,sizeof(p[0]),cmp);
	if(p[0]==0)//如果最大值为0，则说明没有负数，且已经递归完成
		return true;
	for (int i=1;i<=p[0];i++)
	{
		p[i]-=1;
		if(p[i]<0)//有负数，就直接退出即可，减小计算量
			return false;
	}
	p[0]=0;
	if(!havel(p,len))//递归
		return false;
	return true;
}

这里需要加入头文件#include<stdlib.h>

1.在至少含有两个顶点的简单图中，一定有两个顶点的度相同。

证明：

条件：有孤立点时，除去孤立点，即图中所有度至少为1。此时设顶点数为n

根据简单图的定义可以知道，一个点的度至多有n-1，即在1~n-1之间取值，但有n个点，根据抽屉原理或鸽笼原理可以知道，至少有两个点的度是相同的。

根据这个结论，我们很容易判断,5,4,3,2,1是不可成图的。